|
lu
|
|
lu
|
Simple implementations of PLU factorization. More...
#include <stdio.h>#include <math.h>#include "lu_impls.h"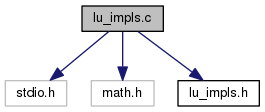
Functions | |
| int | rb_dgetrf (int m, int n, double *A, int lda, int *ipiv) |
Computes the PLU factorization of an m by n matrix A, i.e. 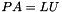 . More... . More... | |
| void | rb_dscal (int n, double a, double *X, int incx) |
Scales a vector by a constant.  . More... . More... | |
| void | rb_dswap (int n, double *X, int incx, double *Y, int incy) |
| Swaps the value of vector X and Y. More... | |
| void | rb_daxpy (int n, double a, const double *X, int incx, double *Y, int incy) |
Scale a vector X by a constant add add it to another vector Y. 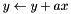 . More... . More... | |
| int | rb_idamax (int n, double *X, int incx) |
| Finds the index of the element in X which has the maximum absolute value. More... | |
Simple implementations of PLU factorization.
| void rb_daxpy | ( | int | n, |
| double | a, | ||
| const double * | X, | ||
| int | incx, | ||
| double * | Y, | ||
| int | incy | ||
| ) |
Scale a vector X by a constant add add it to another vector Y. 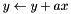 .
.
| n | The length of X and Y. |
| a | The scaling constant. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
| Y | Input/Output. The pointer to the storage of Y. |
| incy | The increment of indices of Y. |
| int rb_dgetrf | ( | int | m, |
| int | n, | ||
| double * | A, | ||
| int | lda, | ||
| int * | ipiv | ||
| ) |
Computes the PLU factorization of an m by n matrix A, i.e. 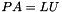 .
.
| m | The number of rows of A. |
| n | The number of columns of A. |
| A | Input/Output. Pointer to the storage of A. |
| lda | The leading dimension of A. |
| ipiv | Output. The integer array that stores the pivoting indices. That is, row i exchanges with row ipiv[i]. |
On exit, R is stored at the upper triangular/trapezoidal part of A, L is stored at the strictly lower triangular/trapezoidal part of A, the diagonal of L is not stored.
For example, suppose A is 4 by 3
![\[ A = \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \\ \end{array}\right) \]](form_1.png)
Then after LU is completed, A is overwritten by
![\[ A = \left(\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\ l_{21} & u_{22} & u_{23} \\ l_{31} & l_{32} & u_{33} \\ l_{41} & l_{42} & l_{43} \\ \end{array}\right) \]](form_2.png)
| void rb_dscal | ( | int | n, |
| double | a, | ||
| double * | X, | ||
| int | incx | ||
| ) |
Scales a vector by a constant.  .
.
| n | The length of X. |
| a | The scaling factor. |
| X | The pointer to the storage of X. |
| incx | The increment of indices. |
| void rb_dswap | ( | int | n, |
| double * | X, | ||
| int | incx, | ||
| double * | Y, | ||
| int | incy | ||
| ) |
Swaps the value of vector X and Y.
| n | The length of X and Y. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
| Y | The pointer to the storage of Y. |
| incy | The increment of indices of Y. |
| int rb_idamax | ( | int | n, |
| double * | X, | ||
| int | incx | ||
| ) |
Finds the index of the element in X which has the maximum absolute value.
| n | The length of X. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
 1.8.11
1.8.11