Simple implementations of conjugate gradient method for solving linear systems.
More...
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "cg_impls.h"
|
| int | rb_dcgsv (int n, Aop A, void *ctxt, const double *b, double *sol) |
| | Solves a linear system using conjugate method. More...
|
| |
| void | rb_dscal (int n, double a, double *X, int incx) |
| | Scales a vector by a constant.  . More... . More...
|
| |
| void | rb_daxpy (int n, double a, const double *X, int incx, double *Y, int incy) |
| | Scale a vector X by a constant add add it to another vector Y. 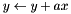 . More... . More...
|
| |
| double | rb_damax (int n, const double *X, int incx) |
| | Finds the element in X which has the maximum absolute value. More...
|
| |
| double | rb_ddot (int n, const double *X, int incx, const double *Y, int incy) |
| | Perform inner product 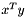 . More... . More...
|
| |
| void | rb_dcopy (int n, const double *X, int incx, double *Y, int incy) |
| | Copy a vector to another. More...
|
| |
| void | rb_dsub (int n, const double *X, int incx, const double *Y, int incy, double *Z, int incz) |
| | Perform vector substraction, i.e. 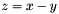 . More... . More...
|
| |
Simple implementations of conjugate gradient method for solving linear systems.
- Author
- RyanBern
| void rb_damax |
( |
int |
n, |
|
|
const double * |
X, |
|
|
int |
incx |
|
) |
| |
Finds the element in X which has the maximum absolute value.
- Parameters
-
| n | The length of X. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
- Returns
- The element which has the maximum absolute value
| void rb_daxpy |
( |
int |
n, |
|
|
double |
a, |
|
|
const double * |
X, |
|
|
int |
incx, |
|
|
double * |
Y, |
|
|
int |
incy |
|
) |
| |
Scale a vector X by a constant add add it to another vector Y. 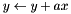 .
.
- Parameters
-
| n | The length of X and Y. |
| a | The scaling constant. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
| Y | Input/Output. The pointer to the storage of Y. |
| incy | The increment of indices of Y. |
| int rb_dcgsv |
( |
int |
n, |
|
|
Aop |
A, |
|
|
void * |
ctxt, |
|
|
const double * |
b, |
|
|
double * |
sol |
|
) |
| |
| void rb_dcopy |
( |
int |
n, |
|
|
const double * |
X, |
|
|
int |
incx, |
|
|
double * |
Y, |
|
|
int |
incy |
|
) |
| |
Copy a vector to another.
- Parameters
-
| n | The length of X and Y. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
| Y | The pointer to the storage of Y. |
| incy | The increment of indices of Y. |
| double rb_ddot |
( |
int |
n, |
|
|
const double * |
X, |
|
|
int |
incx, |
|
|
const double * |
Y, |
|
|
int |
incy |
|
) |
| |
Perform inner product 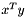 .
.
- Parameters
-
| n | The length of X and Y. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
| Y | The pointer to the storage of Y. |
| incy | The increment of indices of Y. |
- Returns
- The inner product.
| void rb_dscal |
( |
int |
n, |
|
|
double |
a, |
|
|
double * |
X, |
|
|
int |
incx |
|
) |
| |
Scales a vector by a constant.  .
.
- Parameters
-
| n | The length of X. |
| a | The scaling factor. |
| X | The pointer to the storage of X. |
| incx | The increment of indices. |
| void rb_dsub |
( |
int |
n, |
|
|
const double * |
X, |
|
|
int |
incx, |
|
|
const double * |
Y, |
|
|
int |
incy, |
|
|
double * |
Z, |
|
|
int |
incz |
|
) |
| |
Perform vector substraction, i.e. 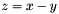 .
.
- Parameters
-
| n | The length of X and Y. |
| X | The pointer to the storage of X. |
| incx | The increment of indices of X. |
| Y | The pointer to the storage of Y. |
| incy | The increment of indices of Y. |
| Z | Output. The pointer to the storage of Z. |
| incy | The increment of indices of Z. |
 . More...
. More...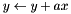 . More...
. More...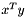 . More...
. More...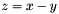 . More...
. More...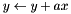 .
. 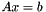 .
. 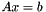 with conjugate gradient method. It requires
with conjugate gradient method. It requires 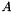 to be positive definite.
to be positive definite.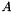 to be given explicitly. It only needs
to be given explicitly. It only needs 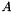 when applying it to a vector. That is, the user only has to tell how to perform
when applying it to a vector. That is, the user only has to tell how to perform 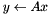 , by providing the parameter of type Aop and all the context needed by the operator.
, by providing the parameter of type Aop and all the context needed by the operator. 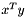 .
.  .
. 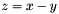 .
.  1.8.11
1.8.11